Quadratic Bézier Curve 0.1.0

前回 2 点間で直線を表しましたが、今回は 3 点を使ってベジエ曲線を表してみましょう。 2 点 $\boldsymbol{v}_1$ と $\boldsymbol{v}_2$ を通る直線 $\boldsymbol{v}_{12}$ をパラメーター $k$ で表すと、 $$\boldsymbol{v}_{12} = (1 - k) \boldsymbol{v}_1 + k \boldsymbol{v}_2 $$ となり、2 点 $\boldsymbol{v}_2$ と $\boldsymbol{v}_3$ を通る直線 $\boldsymbol{v}_{23}$ をパラメーター $k$ で表すと、 $$\boldsymbol{v}_{23} = (1 - k) \boldsymbol{v}_2 + k \boldsymbol{v}_3 $$ となります。これは前回と同様の直線ですが、さらに、この 2 つの通過点の中間点 $$\boldsymbol{v} = (1 - k) \boldsymbol{v}_{12} + k \boldsymbol{v}_{23} $$ は「2 次ベジエ曲線」と呼ばれる曲線になります。2 次ベジエ曲線は両端の $\boldsymbol{v}_1$ と $\boldsymbol{v}_3$ を通りますが、もう 1 つの $\boldsymbol{v}_2$ は通りません。この点を制御点と呼びます。 3 次ベジエ曲線はこの制御点が 2 つになります。

2 次というのはこの曲線が 2 次曲線という意味ではありません。つまり 2 次ベジエ曲線イコール放物線というわけではありません。双曲線のようにも見えますが、一体どのような曲線なのでしょうか。計算を簡単にするために $\boldsymbol{v}_1 = (1, 0)$、$\boldsymbol{v}_2 = (0, 0)$、$\boldsymbol{v}_3 = (0, 1)$ として計算してみましょう。$\boldsymbol{v}_2$ は原点にしたので、掛け算すると消えます。 $$\boldsymbol{v}_{12} = (1 - k) \boldsymbol{v}_1 $$ $$\boldsymbol{v}_{23} = k \boldsymbol{v}_3 $$ $$\boldsymbol{v} = (1 - k)^2 \boldsymbol{v}_1 + k^2 \boldsymbol{v}_3 $$ でこれを縦ベクトルで書き直すと、 $$\begin{pmatrix} x \\ y \end{pmatrix} = (1 - k)^2 \begin{pmatrix} 1 \\ 0 \end{pmatrix} + k^2 \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ つまり、 $$x = (1 - k)^2 $$ $$y = k^2 $$ となります。パラメーター $k$ は $0$ から $1$ まで変化させるので負の値を無視して、 $$k = \sqrt{y} $$ と表せます。一方、$x$ の式も同様に、 $$k - 1 = \sqrt{x} $$ と表せるので、先ほどの式を代入して、 $$\sqrt{y} - 1 = \sqrt{x} $$ $$\sqrt{x} + \sqrt{y} = 1 $$ という式が得られます。これはスーパー楕円と呼ばれる式です。スーパー楕円は実際には $$\left|\frac{x}{a}\right|^n +\left|\frac{y}{b}\right|^n = 1 $$ という式なので、二次ベジエ曲線は $a = b = 1$、$n = 0.5$ のときのスーパー楕円に相当する曲線になります。

実行結果

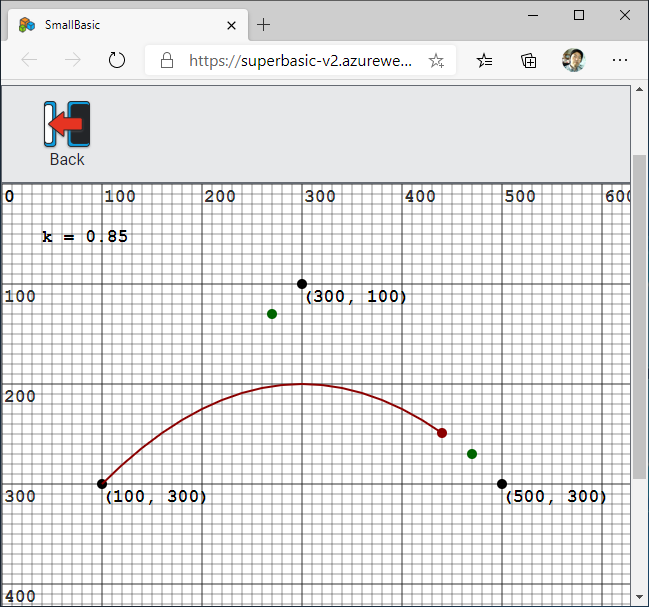
Small Basic オンラインで実行したスクリーンショットを以下に示します。まず、座標 (100, 300)、座標 (300, 100)、座標 (500, 300) に $\boldsymbol{v}_1$ と $\boldsymbol{v}_2$ と $\boldsymbol{v}_3$ を表す黒い点を打っています。下図では $k = 0.85$ のときの $\boldsymbol{v}_{12}$ と $\boldsymbol{v}_{23}$ を緑の点で表示しています。さらに $\boldsymbol{v}$ を赤い点で表示し、その軌跡（ベジエ曲線）も赤で表示しています。

ソース

BezierCurve.txt

プログラムは前回の LineAnime.txt とよく似ています。

12,18,24行目：黒い点を打っています。
28行目：緑の点と赤い点を Shapes.AddEllipse で作成します。
34行目：$k$ を $0.05$ ずつ増やしながら、
35行目：緑の点と赤い点を移動し、
38行目：軌跡の赤い線を Shapes.AddLine で作成します。
45行目：$k$ が $1$ に達した後、赤い線を消します。

' Quadratic Bézier Curve
' Version 0.1.0
' Copyright © 2020 Nonki Takahshi.  The MIT License.
' Last update 2020-08-31
 
DrawGrid()

size = 10   ' size of a point

x = 100
y = 300
DrawPoint()
x1 = x
y1 = y

x = 300
y = 100
DrawPoint()
x2 = x
y2 = y

x = 500
y = 300
DrawPoint()
x3 = x
y3 = y

AddPoints()
GraphicsWIndow.PenWidth = 2
GraphicsWindow.PenColor = "DarkRed"
While "True"
    shL = ""
    nL = 0
    For k = 0 To 1 Step 0.05
        MovePoints()
        If 0 < k Then
            nL = nL + 1
            shL[nL] = Shapes.AddLine(_x, _y, x, y)
        EndIf
        _x = x
        _y = y
        Program.Delay(500)
    EndFor
    For i = 1 To nL
        Shapes.Remove(shL[i])
    EndFor
EndWhile

Sub AddPoints
    shT = Shapes.AddText("")
    Shapes.Move(shT, 40, 40)
    GraphicsWindow.PenWidth = 0
    GraphicsWindow.BrushColor = "DarkGreen"
    shP[1] = Shapes.AddEllipse(size, size)
    shP[2] = Shapes.AddEllipse(size, size)
    GraphicsWindow.BrushColor = "DarkRed"
    shP[3] = Shapes.AddEllipse(size, size)
EndSub

Sub DrawPoint
    GraphicsWindow.BrushColor = "Black"
    GraphicsWindow.FillEllipse(x - size / 2, y - size / 2, size, size)
    GraphicsWindow.DrawText(x, y, "(" + x + ", " + y + ")")
EndSub

Sub DrawGrid
    gw = GraphicsWindow.Width
    gh = GraphicsWindow.Height
    fn = GraphicsWindow.FontName
    If (fn = "Tahoma") Or (fn = "Segoe UI") Then
        c10 = "#33000000"
        c100 = "#66000000"
        bc = "#CC000000"
    Else    ' for SBO
        c10 = "#00000033"
        c100 = "#00000066"
        bc = "#000000CC"
    EndIf
    GraphicsWindow.FontName = "Courier New"
    GraphicsWindow.FontSize = 18
    GraphicsWindow.BrushColor = bc
    For x = 0 To gw Step 10
        If Math.Remainder(x, 100) = 0 Then
            GraphicsWindow.PenColor = c100
            GraphicsWindow.DrawText(x + 2, 0, x)
        Else
            GraphicsWindow.PenColor = c10
        EndIf
        GraphicsWindow.DrawLine(x, 0, x, gh)
    EndFor
    For y = 0 To gh Step 10
        If Math.Remainder(y, 100) = 0 Then
            GraphicsWindow.PenColor = c100
            GraphicsWindow.DrawText(2, y, y)
        Else
            GraphicsWindow.PenColor = c10
        EndIf
        GraphicsWindow.DrawLine(0, y, gw, y)
    EndFor
EndSub

Sub MovePoints
    Shapes.SetText(shT, "k = " + k)
    x12 = (1 - k) * x1 + k * x2
    y12 = (1 - k) * y1 + k * y2
    Shapes.Move(shP[1], x12 - size / 2, y12 - size / 2)
    x23 = (1 - k) * x2 + k * x3
    y23 = (1 - k) * y2 + k * y3
    Shapes.Move(shP[2], x23 - size / 2, y23 - size / 2)
    x = (1 - k) * x12 + k * x23
    y = (1 - k) * y12 + k * y23
    Shapes.Move(shP[3], x - size / 2, y - size / 2)
EndSub