Superellipse 0.1.0

前回ベジエ曲線はスーパー楕円の $n = 0.5$ の形だという話をしました。今回はスーパー楕円を描くプログラムを描いてみました。スーパー楕円の式は $$\left|\frac{x}{a}\right|^n +\left|\frac{y}{b}\right|^n = 1 $$ ですが、このままでは計算しずらいので、パラメーター $\theta$ を使って表します。 $$\DeclareMathOperator{\sgn}{sgn} x = \sgn(\cos \theta) \; a \; \left| \cos \theta \right| ^{\frac{2}{n}} $$ $$ y = \sgn(\sin \theta ) \; b \; \left| \sin \theta \right| ^{\frac{2}{n}} $$ ただし符号関数、 $$ \sgn(w) = \begin{cases} -1, & w \lt 0 \\ 0, & w = 0 \\ +1, & w \gt 0 \end{cases} $$ となります。

実行結果

Small Basic オンラインで実行したスクリーンショットを以下に示します。 $a = 1.2$、$b = 1$ に固定しました。 $n = 0.5$ のときは星形となり、ベジエ曲線と同じ形になります。$n = 1.0$ のときはひし形になります。 $n = 2.0$ のときは楕円となり、$n > 2.0$ で長方形に近づいていきます。

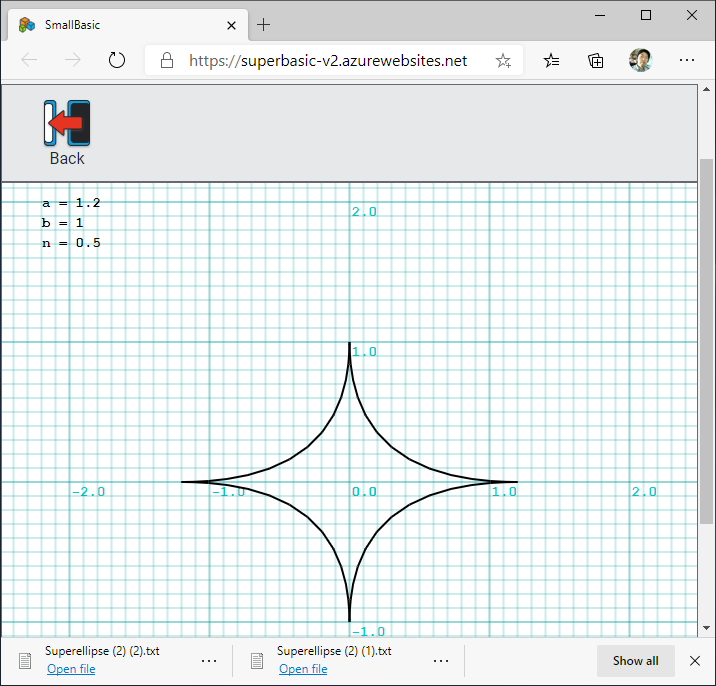
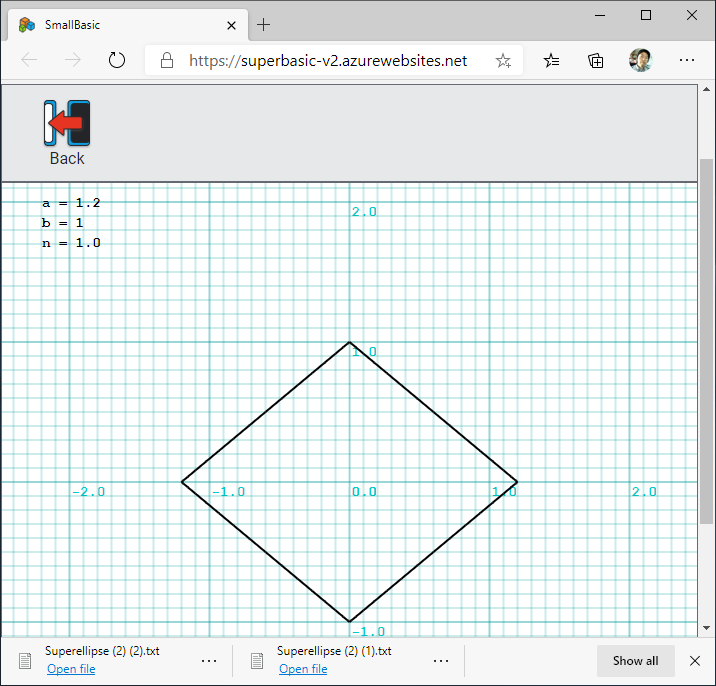
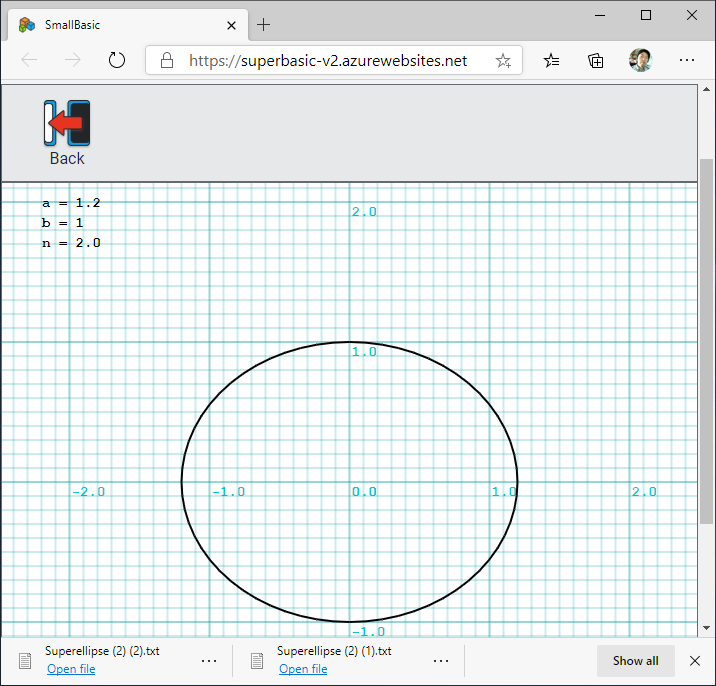
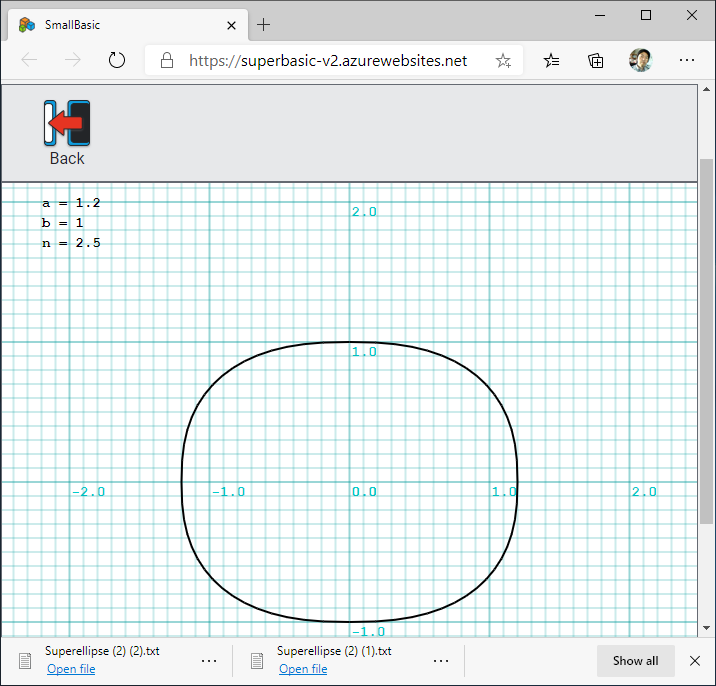
ソース

Superellipse.txt

今回は座標系を数学で使う（原点が中心にあり、$y$ 座標が上向きの）ものにするために Map と MapInv というグラフィックスの座標系と相互に変換するサブルーチンを用意しました。スーパー楕円は上記のパラメーター $\theta$ による式で計算しています。

8,11行目：$a = 1.2$、$b = 1$ に固定します。
16行目：$n$ を $0.5$ ずつ増やしながら、
19行目：前回の $n$ でのスーパー楕円を消し、
23行目：現在の $n$ でのスーパー楕円を描きます。
43,50行目：パラメーター $\theta$ からスーパー楕円を計算します。
120,121行目：数学の座標系をグラフィックスの座標系に変換します。
125,126行目：グラフィックスの座標系を数学の座標系に変換します。

' Superellipse
' Version 0.1.0
' Copyright © 2020 Nonki Takahshi.  The MIT License.
' Last update 2020-09-01

scale = 140
DrawGrid()
a = 1.2
GraphicsWindow.BrushColor = "Black"
GraphicsWindow.DrawText(40, 10, "a = " + a)
b = 1
GraphicsWindow.DrawText(40, 30, "b = " + b)
shN = Shapes.AddText("")
Shapes.Move(shN, 40, 50)
While "True"
    For n = 0.5 To 2.5 Step 0.5
        Shapes.SetText(shN, "n = " + n)
        For i = 1 To nL
            Shapes.Remove(shL[i])
        EndFor
        GraphicsWindow.PenWidth = 2
        GraphicsWindow.PenColor = "Black"
        DrawSuperEllipse()
        keyDown = "False"
        Program.Delay(3000)
    EndFor
EndWhile

Sub DrawSuperEllipse
    ' param gxo, gyo - center position in the graphics window
    ' param a, b - major and minor semi axis
    ' param n
    ' param scale
    nL = 0
    shL = ""
    For θ = -Math.Pi To Math.Pi Step Math.Pi / 32
        abs = Math.Abs(Math.Cos(θ))
        If abs = 0 Then
            sgn = 0
        Else
            sgn = Math.Cos(θ) / abs
        EndIf
        x = sgn * a * Math.Power(abs, 2 / n)
        abs = Math.Abs(Math.Sin(θ))
        If abs = 0 Then
            sgn = 0
        Else
            sgn = Math.Sin(θ) / abs
        EndIf
        y = sgn * b * Math.Power(abs, 2 / n)
        Map()
        gx2 = gx
        gy2 = gy
        If gx1 <> "" Then
            nL = nL + 1
            shL[nL] = Shapes.AddLine(gx1, gy1, gx2, gy2)
            Program.Delay(100)
        EndIf
        gx1 = gx2
        gy1 = gy2
    EndFor
EndSub

Sub DrawGrid
    gw = GraphicsWindow.Width
    gh = GraphicsWindow.Height
    gxo = gw / 2
    gyo = gh / 2
    fn = GraphicsWindow.FontName
    If (fn = "Tahoma") Or (fn = "Segoe UI") Then
        c10 = "#33009999"
        c100 = "#66009999"
        bc = "#00CCCC"
    Else    ' for SBO
        c10 = "#00999933"
        c100 = "#00999966"
        bc = "#00CCCC"
    EndIf
    GraphicsWindow.FontName = "Courier New"
    GraphicsWindow.FontSize = 14
    GraphicsWindow.BrushColor = bc
    dx = 0.1
    dy = -0.1
    gx = Math.Remainder(gw / 2, dx * scale)
    gy = Math.Remainder(gh / 2, dy * scale)
    MapInv()
    x1 = x
    y1 = y
    gx = gw - Math.Remainder(gw / 2, 10)
    gy = gh - Math.Remainder(gh / 2, 10)
    MapInv()
    x2 = x
    y2 = y
    For x = x1 To x2 Step dx
        Map()
        rem = Math.Remainder(x, 1)
        If rem = 0.0 Then
            GraphicsWindow.PenColor = c100
            GraphicsWindow.DrawText(gx + 2, gh / 2, x)
        Else
            GraphicsWindow.PenColor = c10
        EndIf
        GraphicsWindow.DrawLine(gx, 0, gx, gh)
    EndFor
    For y = y1 To y2 Step dy
        Map()
        If Math.Remainder(y, 1) = 0.0 Then
            GraphicsWindow.PenColor = c100
            If y <> 0 Then
            GraphicsWindow.DrawText(gw / 2 + 2, gy, y)
            EndIf
        Else
            GraphicsWindow.PenColor = c10
        EndIf
        GraphicsWindow.DrawLine(0, gy, gw, gy)
    EndFor
EndSub

Sub Map
    gx = gxo + scale * x
    gy = gyo - scale * y
EndSub

Sub MapInv
    x = (gx - gxo) / scale
    y = -(gy - gyo) / scale
EndSub