Small Basicで学ぶプログラミング 目次 > 本文

Cubic Bézier Curve 0.1.0

2 次ベジエ曲線は 3 点を使いましたが、3 次ベジエ曲線は 4 点を使います。 2 点 $\boldsymbol{v}_1$ と $\boldsymbol{v}_2$ を通る直線 $\boldsymbol{v}_{12}$ をパラメーター $k$ で表すと、 $$\boldsymbol{v}_{12} = (1 - k) \boldsymbol{v}_1 + k \boldsymbol{v}_2 $$ となり、2 点 $\boldsymbol{v}_2$ と $\boldsymbol{v}_3$ を通る直線 $\boldsymbol{v}_{23}$ をパラメーター $k$ で表すと、 $$\boldsymbol{v}_{23} = (1 - k) \boldsymbol{v}_2 + k \boldsymbol{v}_3 $$ となり、2 点 $\boldsymbol{v}_3$ と $\boldsymbol{v}_4$ を通る直線 $\boldsymbol{v}_{34}$ をパラメーター $k$ で表すと、 $$\boldsymbol{v}_{34} = (1 - k) \boldsymbol{v}_3 + k \boldsymbol{v}_4 $$ となります。これらは前回と同様の直線ですが、直線 $\boldsymbol{v}_{12}$ と 直線 $\boldsymbol{v}_{23}$ の $k$ のときの2点を結ぶ直線の $k$ のときの中間点 $$\boldsymbol{v}_{13} = (1 - k) \boldsymbol{v}_{12} + k \boldsymbol{v}_{23} $$ および、直線 $\boldsymbol{v}_{23}$ と直線 $\boldsymbol{v}_{34}$ の $k$ のときの2点を結ぶ直線の $k$ のときの中間点 $$\boldsymbol{v}_{24} = (1 - k) \boldsymbol{v}_{12} + k \boldsymbol{v}_{23} $$ はそれぞれ 2 次ベジエ曲線になり、さらにこれらの $k$ のときの中間点 $$\boldsymbol{v} = (1 - k) \boldsymbol{v}_{13} + k \boldsymbol{v}_{24} $$ が 3 次ベジエ曲線になります。

さてこの 3 次ベジエ曲線は一体どのような曲線なのでしょうか。まずは計算を簡単にするために $\boldsymbol{v}_1 = (-1, 0)$、$\boldsymbol{v}_2 = (-1/3, 4/3)$、$\boldsymbol{v}_3 = (1/3, -4/3)$、 $\boldsymbol{v}_4 = (1, 0)$ として計算してみましょう。 $$\boldsymbol{v}_{12} = (1 - k) \begin{pmatrix} -1 \\ 0 \end{pmatrix} + k \begin{pmatrix} -\frac{1}{3} \\ \frac{4}{3} \end{pmatrix} = \begin{pmatrix} \frac{2}{3}k - 1 \\ \frac{4}{3}k \end{pmatrix} $$ $$\boldsymbol{v}_{23} = (1 - k) \begin{pmatrix} -\frac{1}{3} \\ \frac{4}{3} \end{pmatrix} + k \begin{pmatrix} \frac{1}{3} \\ -\frac{4}{3} \end{pmatrix} = \begin{pmatrix} \frac{2}{3}k - \frac{1}{3} \\ \frac{4}{3} - \frac{8}{3}k \end{pmatrix} $$ $$\boldsymbol{v}_{34} = (1 - k) \begin{pmatrix} \frac{1}{3} \\ -\frac{4}{3} \end{pmatrix} + k \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} \frac{1}{3} + \frac{2}{3}k \\ \frac{4}{3}k - \frac{4}{3} \end{pmatrix} $$ でこれを 2 次ベジエ曲線の式に代入すると、 $$\boldsymbol{v}_{13} = (1 - k) \begin{pmatrix} \frac{2}{3}k - 1 \\ \frac{4}{3}k \end{pmatrix} + k \begin{pmatrix} \frac{2}{3}k - \frac{1}{3} \\ \frac{4}{3} - \frac{8}{3}k \end{pmatrix} = \begin{pmatrix} \frac{4}{3}k - 1 \\ -4k^2 + \frac{8}{3}k \end{pmatrix} $$ $$\boldsymbol{v}_{24} = (1 - k) \begin{pmatrix} \frac{2}{3}k - \frac{1}{3} \\ \frac{4}{3} - \frac{8}{3}k \end{pmatrix} + k \begin{pmatrix} \frac{1}{3} + \frac{2}{3}k \\ \frac{4}{3}k - \frac{4}{3} \end{pmatrix} = \begin{pmatrix} \frac{4}{3}k - \frac{1}{3} \\ 4k^2 - \frac{16}{3}k + \frac{4}{3} \end{pmatrix} $$ となります。さらに 3 次ベジエ曲線の式は、 $$\begin{pmatrix} x \\ y \end{pmatrix} = (1 - k) \begin{pmatrix} \frac{4}{3}k - 1 \\ -4k^2 + \frac{8}{3}k \end{pmatrix} + k \begin{pmatrix} \frac{4}{3}k - \frac{1}{3} \\ 4k^2 - \frac{16}{3}k + \frac{4}{3} \end{pmatrix} $$ $$ = \begin{pmatrix} 2k - 1 \\ 8k^3 - 12k^2 + 4k \end{pmatrix} $$ つまり、 $$x = 2k - 1 $$ $$y = 8k^3 - 12k^2 + 4k $$ となります。この式からパラメーター $k$ を消したいので、$x$ の式から $$k = \frac{x + 1}{2} $$ として、$y$ の式に代入し、 $$y = 8 \left( \frac{x + 1}{2} \right)^3 -12 \left( \frac{x + 1}{2} \right)^2 + 4 \left( \frac{x + 1}{2} \right) $$ $$ = x^3 + 3x^2 + 3x + 1 - 3(x^2 + 2x + 1) + 2(x + 1) $$ $$ = x^3 - x $$ となり、3次曲線の式が得られます。

他に3次ベジエ曲線でどんな曲線が描けるか、例をまとめてみました。プログラムは今回省略します。

スーパー楕円 (superellipse)

$\boldsymbol{v}_1 = (1, 0), \boldsymbol{v}_2 = (0, 0), \boldsymbol{v}_3 = (0, 0), \boldsymbol{v}_4 = (0, 1)$ のとき $|x|^{\frac{1}{3}} + |y|^{\frac{1}{3}} = 1$ という式のスーパー楕円を描けます。2次ベジエのときは $n = 0.5$ でしたが、 3次ベジエでは $n = \frac{1}{3}$ になりました。

半3次放物線 (semicubic parabola)

$\boldsymbol{v}_1 = (1, \sqrt{a}), \boldsymbol{v}_2 = (-\frac{1}{3}, -\sqrt{a}), \boldsymbol{v}_3 = (-\frac{1}{3}, \sqrt{a}), \boldsymbol{v}_4 = (1, -\sqrt{a})$ のとき $y^2 = ax^3$ という式の半3次放物線を描けます。「く」の字形の曲線です。

チルンハウス3次曲線 (Tschirnhausen cubic)

$\boldsymbol{v}_1 = (1, 2), \boldsymbol{v}_2 = (-4\frac{1}{3}, -10), \boldsymbol{v}_3 = (-4\frac{1}{3}, 10), \boldsymbol{v}_4 = (1, -2)$ のとき $y^2 = x^3 + 3x^2$ という式のチルンハウス3次曲線を描けます。「$\alpha$」形の曲線です。

実行結果

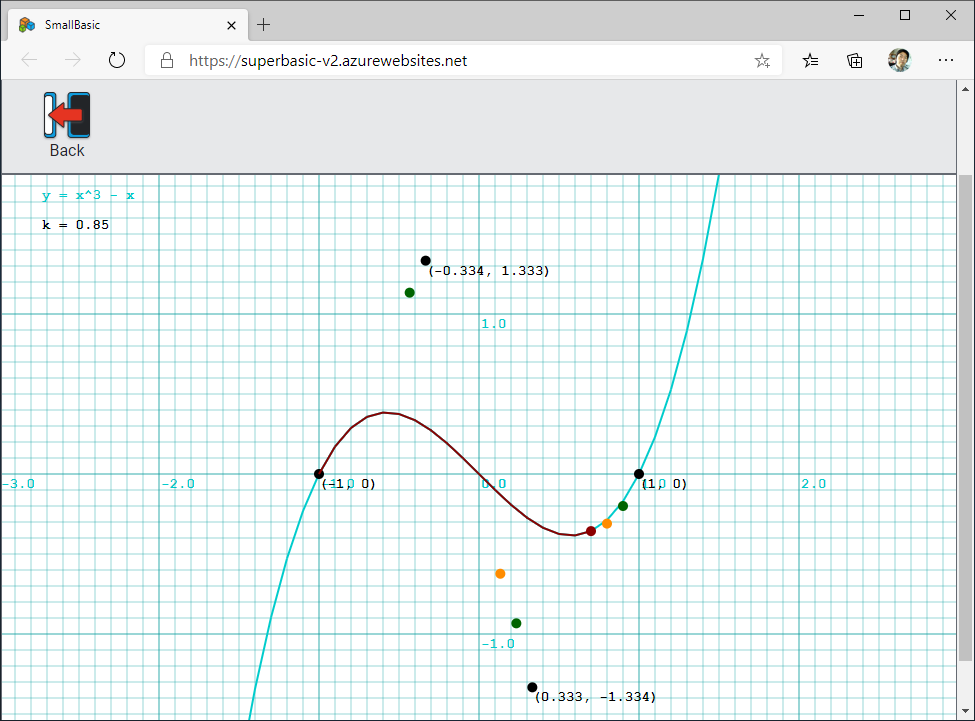
Small Basic オンラインで実行したスクリーンショットを以下に示します。 まず、$y = x^3 - x$ のグラフを水色で描きます。その上に、座標 (-1, 0)、座標 (-1/3, 4/3)、座標 (1/3, -4/3)、 座標 (1, 0) に $\boldsymbol{v}_1$ と $\boldsymbol{v}_2$ と $\boldsymbol{v}_3$ と $\boldsymbol{v}_4$ を表す黒い点を打ちます。 下図では $k = 0.85$ のときの $\boldsymbol{v}_{12}$ と $\boldsymbol{v}_{23}$ と $\boldsymbol{v}_{34}$ を緑の点で表示しています。また、$\boldsymbol{v}_{13}$ と $\boldsymbol{v}_{24}$ をオレンジ の点で表示しています。 さらに $\boldsymbol{v}$ を赤い点で表示し、その軌跡（ベジエ曲線）も赤で表示しています。 赤いベジエ曲線が水色の3次曲線グラフと一致するのが解ります。

ソース

CubicBezier.txt

2次ベジエ曲線 BezierCurve.txt のときはグラフィックの座標系を使っていましたが、今回は数式に沿って表示 したかったので、3次ベジエ曲線にも Map を使って座標変換しています。

• 11～14行目：3次式に与える係数を設定しています。
• 16行目：左上に表示する3次式の文字列 expr を求めています。
• 50行目：3次ベジエ曲線を求め、緑、オレンジ、赤の点を移動します。
• 53行目：軌跡の赤い線を Shapes.AddLine で作成します。
• 231行目以降：Map を呼び出しているところをハイライトしました。

' Cubic Bézier Curve
' Version 0.1.0
' Copyright © 2020 Nonki Takahshi.  The MIT License.
' Last update 2020-09-10
 
scale = 150
DrawGrid()

size = 10   ' size of a point [pixel]

a = 1
b = 0
c = -1
d = 0
DrawCubic()
Expression()
GraphicsWindow.DrawText(40, 10, expr)

x = -1
y = 0
DrawPoint()
x1 = x
y1 = y

x = -1/3
y = 4/3
DrawPoint()
x2 = x
y2 = y

x = 1/3
y = -4/3
DrawPoint()
x3 = x
y3 = y

x = 1
y = 0
DrawPoint()
x4 = x
y4 = y

AddPoints()
GraphicsWIndow.PenWidth = 2
GraphicsWindow.PenColor = "DarkRed"
While "True"
    shL = ""
    nL = 0
    For k = 0 To 1 Step 0.05
        MovePoints()
        If 0 < k Then
            nL = nL + 1
            shL[nL] = Shapes.AddLine(_gx, _gy, gx, gy)
        EndIf
        _gx = gx
        _gy = gy
        Program.Delay(100)
    EndFor
    For i = 1 To nL
        Shapes.Remove(shL[i])
    EndFor
EndWhile

Sub AddPoints
    shT = Shapes.AddText("")
    Shapes.Move(shT, 40, 40)
    GraphicsWindow.PenWidth = 0
    GraphicsWindow.BrushColor = "DarkGreen"
    shP[1] = Shapes.AddEllipse(size, size)
    shP[2] = Shapes.AddEllipse(size, size)
    shP[3] = Shapes.AddEllipse(size, size)
    GraphicsWindow.BrushColor = "DarkOrange"
    shP[4] = Shapes.AddEllipse(size, size)
    shP[5] = Shapes.AddEllipse(size, size)
    GraphicsWindow.BrushColor = "DarkRed"
    shP[6] = Shapes.AddEllipse(size, size)
EndSub

Sub Cubic
    y = a * x * x * x + b * x * x + c * x + d
EndSub

Sub DrawCubic
    ' param gxo, gyo - center position in the graphics window
    ' param a, b - major and minor semi axis
    ' param n
    ' param scale
    GraphicsWIndow.PenColor = "#00CCCC"
    For x = x1 To x2 Step dx
        Cubic()
        Map()
        gx2 = gx
        gy2 = gy
        If x <> x1 Then
            GraphicsWindow.DrawLine(gx1, gy1, gx2, gy2)
        EndIf
        gx1 = gx2
        gy1 = gy2
    EndFor
EndSub

Sub DrawGrid
    gw = GraphicsWindow.Width
    gh = GraphicsWindow.Height
    gxo = gw / 2
    gyo = gh / 2
    fn = GraphicsWindow.FontName
    If (fn = "Tahoma") Or (fn = "Segoe UI") Then
        c10 = "#33009999"
        c100 = "#66009999"
        bc = "#00CCCC"
    Else    ' for SBO
        c10 = "#00999933"
        c100 = "#00999966"
        bc = "#00CCCC"
    EndIf
    GraphicsWindow.FontName = "Courier New"
    GraphicsWindow.FontSize = 14
    GraphicsWindow.BrushColor = bc
    dx = 0.1
    dy = -0.1
    gx = Math.Remainder(gw / 2, dx * scale) - dx * scale
    gy = Math.Remainder(gh / 2, dy * scale)
    MapInv()
    x1 = x
    y1 = y
    gx = gw - Math.Remainder(gw / 2, dx * scale) + dx * scale
    gy = gh - Math.Remainder(gh / 2, dy * scale)
    MapInv()
    x2 = x
    y2 = y
    For x = x1 To x2 Step dx
        Map()
        rem = Math.Remainder(x, 1)
        If rem = 0.0 Then
            GraphicsWindow.PenColor = c100
            GraphicsWindow.DrawText(gx + 2, gh / 2, x)
        Else
            GraphicsWindow.PenColor = c10
        EndIf
        GraphicsWindow.DrawLine(gx, 0, gx, gh)
    EndFor
    For y = y1 To y2 Step dy
        Map()
        If Math.Remainder(y, 1) = 0.0 Then
            GraphicsWindow.PenColor = c100
            If x <> 0 Then
                GraphicsWindow.DrawText(gw / 2 + 2, gy, y)
            EndIf
        Else
            GraphicsWindow.PenColor = c10
        EndIf
        GraphicsWindow.DrawLine(0, gy, gw, gy)
    EndFor
EndSub

Sub DrawPoint
    GraphicsWindow.BrushColor = "Black"
    Map()
    GraphicsWindow.FillEllipse(gx - size / 2, gy - size / 2, size, size)
    _x = Math.Floor(x * 1000) / 1000
    _y = Math.Floor(y * 1000) / 1000
    GraphicsWindow.DrawText(gx, gy, "(" + _x + ", " + _y + ")")
EndSub

Sub Expression
    expr = "y ="
    plus = " "
    If a = 1 Then
        expr = expr + " x^3"
        plus = " + "
    ElseIf a = -1 Then
        expr = expr + " - x^3"
        plus = " + "
    ElseIf a <> 0 Then
        expr = expr + " " + a + " * x^3"
        plus = " + "
    EndIf
    If b = 1 Then
        expr = expr + plus + "x^2"
        plus = " + "
    ElseIf b = -1 Then
        expr = expr + " - x^2"
        plus = " + "
    ElseIf 0 < b Then
        expr = expr + plus + b + " * x^2"
        plus = " + "
    ElseIf b < 0 Then
        expr = expr + " - " + Math.Abs(b) + " * x^2"
        plus = " + "
    EndIf
    If c = 1 Then
        expr = expr + plus + "x"
        plus = " + "
    ElseIf c = -1 Then
        expr = expr + " - x"
        plus = " + "
    ElseIf 0 < c Then
        expr = expr + plus + c + " * x"
        plus = " + "
    ElseIf c < 0 Then
        expr = expr + " - " + Math.Abs(c) + " * x"
        plus = " + "
    EndIf
    If 0 < d Then
        expr = expr + plus + d
    ElseIf d < 0 Then
        expr = expr + " - " + Math.Abs(d)
    EndIf
    If (a = 0) And (b = 0) And (c = 0) And (d = 0) Then
        expr = expr + " 0"
    EndIf
EndSub

Sub Map
    gx = gxo + scale * x
    gy = gyo - scale * y
EndSub

Sub MapInv
    x = (gx - gxo) / scale
    y = -(gy - gyo) / scale
EndSub

Sub MovePoints
    Shapes.SetText(shT, "k = " + k)
    x12 = (1 - k) * x1 + k * x2
    y12 = (1 - k) * y1 + k * y2
    x = x12
    y = y12
    Map()
    Shapes.Move(shP[1], gx - size / 2, gy - size / 2)
    x23 = (1 - k) * x2 + k * x3
    y23 = (1 - k) * y2 + k * y3
    x = x23
    y = y23
    Map()
    Shapes.Move(shP[2], gx - size / 2, gy - size / 2)
    x34 = (1 - k) * x3 + k * x4
    y34 = (1 - k) * y3 + k * y4
    x = x34
    y = y34
    Map()
    Shapes.Move(shP[3], gx - size / 2, gy - size / 2)
    x13 = (1 - k) * x12 + k * x23
    y13 = (1 - k) * y12 + k * y23
    x = x13
    y = y13
    Map()
    Shapes.Move(shP[4], gx - size / 2, gy - size / 2)
    x24 = (1 - k) * x23 + k * x34
    y24 = (1 - k) * y23 + k * y34
    x = x24
    y = y24
    Map()
    Shapes.Move(shP[5], gx - size / 2, gy - size / 2)
    x = (1 - k) * x13 + k * x24
    y = (1 - k) * y13 + k * y24
    Map()
    Shapes.Move(shP[6], gx - size / 2, gy - size / 2)
EndSub

---

Copyright © 2020 たかはしのんき. All rights reserved.